I want to share a story about how a new idea can originate in a chance hallway conversation. The story is about ecological niches.
When you think about a niche, you might imagine something like you see here in the city of Samarkand: the Mirza-Uluk-Bek in the Registan (one of the first color photographs).
The ecological niche is something different, but draws on the metaphor of a recessed space that can hold something. The concept was primarily popularized by G.E. Hutchinson in the late 1950s, and used to describe species. For him, a niche is
An area is thus defined, each point of which corresponds to a possible environmental state… an n-dimensional hypervolume is defined, every point in which corresponds to a state of the environment which would permit the species.. to exist indefinitely.
This reasonable concept makes intuitive sense: for some set of variables that are important to species, the niche is the combination of variables in which the species can live. You might imagine that a ‘real’ niche simultaneously depends on many variables. Unfortunately the definition says nothing about how to measure one.
This brings us a few decades forward, to early 2012. One morning I left my desk to get a drink of water in the hallway. I ran into Brian Enquist and Christine Lamanna, who were there talking about ecological niches. They asked me if I knew of any algorithms to find the overlap between two niches. I said I didn’t, but I was sure that the problem was solved, and a quick search would resolve the question. We did that search, and after some hours it became clear that the problem was actually not solved. Conceptual debates over what a niche is had for several decades obscured the issue of how to measure one.
The trouble is that a niche probably has many dimensions, and the mathematics get bad very quickly. Thinking about the geometry of a high-dimensional object is fundamentally different than thinking about a low-dimensional object. We were surprised by how hard the problem seemed, but also that no one had yet solved it. So we set ourselves the challenge of finding a more efficient way to determine the shape and overlap of high-dimensional ecological niches. We decided to do a thresholded kernel density estimation, which amounts to taking a set of observations of all variables, estimating their overall probability density, then slicing through this density to determine the ‘edge’ of the niche. You can see this illustrated in one dimension below.
Finding a computationally fast way to do this was a challenge. Over the next few months, I wrote five or six different algorithms based on different ideas. Most were a complete failure or were computationally too slow to be effective in more than two or three dimensions. Here’s an early version based on range box-intersections.
And here’s another version, some weeks later – after I discovered an idea that would form the basis of our final solution.
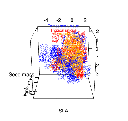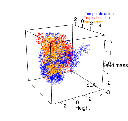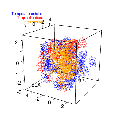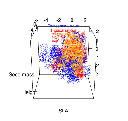
The core innovation is that the entire niche space doesn’t have to be sampled. A good algorithm can avoid doing calculations in the vast regions of niche space that are almost surely ‘out’, and focus instead on the regions that might be ‘in’. The tradeoff is that the niche is only defined in a stochastic sense. We only get approximate answers but we can get them quickly, and can easily visualize the shape and volume of an arbitrary complex niche in any number of dimensions.
I was able to get a usable version working in MATLAB, and after another few weeks of work, rewrote all the code in R, a more commonly used statistical programming language. I won’t go into all the details of the underlying mathematics, but will simply say that everything works – and for reasonably sized datasets, answers can be obtained in seconds or minutes.
Here’s an example of what the algorithms can do. Below you are seeing a three-dimensional niche, the functional hypervolume of tree species in the temperate (blue) or tropical biomes (red) of the New World. The overlapped hypervolume is in orange. We are now able to determine exactly what resources and strategies are unique or shared in different parts of the world.
We had a rough time getting the method published – niches are controversial because of their central importance in ecology. But after some discouraging rejections, our paper is now out! Check it out in Global Ecology and Biogeography (PDF version here). The issues around niche concepts and niche measurement are more complex than I have presented in this short blog post, and I encourage you to read the paper for a full exploration of the topic. As for the algorithms, they are freely available as the ‘hypervolume’ package on CRAN and come with documentation and demonstration analyses.
Here’s an example (in R) of how to use the code – just a few lines to analyze and visualize a complex multidimensional dataset.
I hope these algorithms will open up a whole new range of analyses that weren’t possible before. It has been a long road to see our work come out – and all thanks to a lucky hallway conversation, good collaborators, and the stubbornness to believe that some things that look impossible are not.






Comments
20 responses to “The ecological niche and the n-dimensional hypervolume”
(I apologize if this shows up twice. I wasn’t sure it went through the first time)
Hey Ben, thanks for writing this up. I haven’t read the paper too closely yet, but I’ve enjoyed what I’ve seen so far.
One thing has been nagging at me since I saw this the other day, and I was wondering what your thoughts were.
The underlying kernel density estimates fall off smoothly, and (probably) species’ actual responses to the environment do as well. Thus, even if no other approximations were involved, dropping from the continuously varying kernel density estimate down to one bit (in or out) destroys potentially valuable information. So why do the thresholding step at all?
It seems like most of the things you can do with a hypervolume would also be possible with the underlying continuous estimates. For example, Warren et al. quantified overlap using Hellinger distance: http://www.danwarren.net/Warren%20et%20al%202008%20Niche%20conservatism.pdf The set operations seem like they would have corresponding methods as well (i.e. adding or subtracting the densities, thresholding at zero where needed).
I’m especially nervous about this because it seems like there could actually be quite a lot of uncertainty about where to put the boundaries. Small changes in the density estimates could lead to very large shifts in the boundaries, which would completely change the interpretation even if the underlying process hardly changed. Have you done any analyses (e.g. bootstrapping) to see if this is a problem?
Thanks for considering my thoughts.
PS your Monte Carlo approach reminds me a bit of slice sampling (http://en.wikipedia.org/wiki/Slice_sampling). Have you thought about how it compares with your importance sampling approach?
Hi,
Thanks for your thoughts on the thresholding. The underlying reason is independent of the smoothness of the density estimate. We need to define the boundary of an object, and ‘slicing’ through the density is the simplest method. We don’t want to use the extra density information once we’ve done the thresholding because the density values are not comparable between big and small objects, because probability density functions are constrained to sum to unity over all space. That means an object with 2x the volume will on average have density values that are 2x lower. The thresholding effectively equally privileges all points and solves this issue. I think that this problem is relevant to the Hellinger distance you mention from the Warren et al. study, so our approach effectively becomes an alternative way to compare distributions.
The other thought is that our density estimates are not actually smooth – they are jagged, because of the use of hyperbox kernels. I agree that smoother kernels would be much better but for a variety of computational reasons I implemented the code as-is. Making this approximation was the only way (as far as we have been able to discover) of doing the density estimates on large high-dimensional datasets quickly.
It is true that the choice of threshold will potentially have a very large effect on the boundaries. We suggest using a consistent algorithm for choosing the threshold, or additionally checking the sensitivity of the qualitative / inferential result to threshold value. In many of the datasets we have worked with so far, there doesn’t appear to be a strong effect – but of course it will depend on what data you are analyzing.
Thanks for passing on the information on slice sampling. It’s a new approach for me but on first glance, it looks like the hard part of the problem is ‘slicing’ through the density function, especially in high dimensions. I think our approach effectively finds an efficient way to do this slicing (calculating of different threshold values) – but we will definitely look into this more to see if we can extend our approach.
Thanks for your reply. I’m still stuck on this:
>We need to define the boundary of an object
I still haven’t seen a reason why we need to do this. If differences in the average heights of densities bother you, you can correct for it using their entropies without thresholding anything.
>It is true that the choice of threshold will potentially have a very large effect on the boundaries
Sorry if I wasn’t clear. That wasn’t what I was concerned about. Let me try again. Given a choice of threshold, small perturbations in the density estimates can lead to large changes in the boundary position. I’ve included a concrete example below. Two bootstrapped hypervolumes only overlap by about a third or so, even though they’re coming from the same underlying distribution.
I believe I followed best practices with this example (e.g. estimating bandwidths like you did in the finch demo, using as many samples as I could without crashing my machine). Assuming that I didn’t make any glaring errors here, I’m really concerned about the quality of these hypervolumes.
PS If ecologists really do need hypervolumes, it would probably be best if they used a method that found the boundary directly, rather than going through the computationally expensive and approximate sampling steps used here. Why not a one-class SVM? http://rvlasveld.github.io/blog/2013/07/12/introduction-to-one-class-support-vector-machines/
#################################
library(dismo)
library(hypervolume)
data(Anguilla_train)
set.seed(1) # Set seed for reproducibility
# Pull out environmental variables where eel was present and scale.
# Drop non-environmental variables, factors, & columns with missing values
x = scale(
Anguilla_train[Anguilla_train$Angaus == 1, -c(1, 2, 13, 14)]
)
# Two bootstrap samples of included rows
x1 = x[sample.int(nrow(x), replace = TRUE), ]
x2 = x[sample.int(nrow(x), replace = TRUE), ]
# find hypervolumes for both bootstrap samples
v1 <- hypervolume(
x1,
bandwidth = estimate_bandwidth(x1),
reps=20000,
quantile=0
)
v2 <- hypervolume(
x2,
bandwidth = estimate_bandwidth(x2),
reps=20000,
quantile=0
)
set = hypervolume_set(v1, v2, reduction_factor=.05, check_memory=FALSE)
# Check overlap between hypervolumes: should be close to one.
set@HVList$Intersection@Volume / v2@Volume
set@HVList$Intersection@Volume / v1@Volume
Hi Dave,
Thanks for engaging with our paper and providing this critical counterpoint for our work. We have been hoping that the paper would produce a broad examination of these algorithms and ideas.
First, with your example – I can duplicate the issue you are bringing up. I will note that if you increase the reduction_factor in hypervolume_set to larger values the inferred overlap does increase. Otherwise, the issue you mention is real. If you experiment with reducing the dimensionality of the input data the overlap values will also increase. I think part of the low overlap is that in a high dimensionality dataset with sparse observations (10 dimensions, 200 observations) the ‘curse of dimensionality’ results in lower fractional overlap values – small errors in each dimension can propagate quickly. For example, if volumes are mis-sampled by 5 percent in each direction, then the overall error will be 1-(1-0.05)^10 = 40% regardless of the algorithm.
Of course, this doesn’t necessarily help the user. I think you raise a good point that systematic study of error and bias as functions of dataset size and quality would be very useful. We didn’t do that comprehensively in the paper we have published, but we have a few collaborators who are beginning to do this sort of work, comparing this algorithm to others (in the context of functional diversity). I think this is important work, because our approach is a new and relatively untested one that may have some downsides like what you have pointed out. If you are interested in being involved, please send me an email separately.
Second, more philosophically – I do think it is true that something like a one-class SVM may give better boundary delineation according to a more objective criterion. However, our approach is fundamentally aimed at doing something different than classification. We are trying to do geometry operations, determining how much hyperspace a set of points takes up, and how different sets interact with each other. As far as I am aware, these related problems are not easily solved by a classification algorithm. Our approach is aimed at unifying different aspects of the Hutchinsonian niche. It may be that this niche concept is problematic even when measureable, and should be rejected – but that is the debate we hope to provoke. If you have further insight, I would be interested in learning more. We who have co-authored this hypervolume paper are certainly not SVM experts and primarily wrote our approach to solve a problem that seemed to be unsolved.
Ben
Hey Ben, thanks for your reply.
I think part of the issue may have to do with the bandwidth being too small for the data I used. In 10 dimensions, everything is pretty far away, and the settings I used seemed to be putting very small boxes around the data points. If each data point got its own box, I *think* we’d expect to see 37% overlap (1/e), which isn’t too far from what I was getting.
Adding data points might help, but I think I’d have to cut the number of samples to make it all fit in memory, so the benefit might end up being smaller than one would hope. Especially since the effects of increasing dimensionality are exponential. Ten dimensions might be about six too many for any reasonably-sized data set with this method.
I don’t have much experience with SVMs either, but I do think that some kind of implicit change of basis (like the kernel trick) would probably be necessary to get acceptable performance on data sets like the one I tried.
The nice thing about an efficient classifier like an SVM is you can tell pretty much *instantly* whether a point is inside or outside the boundary. No mucking around with density boxes needed. So you could just throw 10^8 random points at the classifier in one minute, discarding the vast majority of the points because they fell outside the boundary. Or maybe just keep sampling until you get 10,000 points inside. Either way, you now know the proportion of volume inside the boundary relative to the volume of the random points. You could look for intersections and unions the same way: if it’s inside both, that’s the intersection; if inside either, that’s the union. There are probably more efficient ways to do this, but the nice thing about this approach is that it should work with any kernel. No need to muck around with bounding boxes and importance sampling, and I’d actually trust the estimates much better.
The downside is that you don’t get a probability density, but I don’t think you were really using that anyway.
Hi Dave,
I think you might be right about the bandwidth issue. I don’t think I follow with the 1/e overlap though – can you explain?
Adding more datapoints should cause a O(n^2) scaling for memory and time complexity. Adding more dimensions should be somewhere between O(nlogn) and O(n^2) based on expected performance of a k-d recursive partitioning tree. We’ve done simulation tests (not presented in the MS, but I can email to yo if interested) that support this theoretical expectation. So I do think that, at least computationally, our approach is viable.
I agree that SVM is probably a better classifier right away. However there isn’t a good way to do efficient sampling – what you are proposing will work very poorly on high-dimensional data because nearly all random points will be classified ‘out’, resulting in geometric scaling with the number of dimensions. This simple sampling approach is what we first tried and it was immediately clear that it scaled very badly.
With regard to 1/e: it looks like I mangled the math and didn’t notice my error because the correct answer (40%) happens to be similar to what I was expecting (37%). Here’s what I should have said:
I sampled the data points with replacement (bootstrapping) in my example. We’d expect to find 63.2% of the data points in sample #1 and an overlapping set of about 63.2% of the data points in sample #2. (The 63.2% number comes from 1-1/e, see e.g. here: http://cindy.informatik.uni-bremen.de/cosy/teaching/CM_2011/Eval3/efron_97.pdf).
So if 63.2% of the points are in #1 and an independent set of 63.2% are in sample 2, then we’d expect about 40% of the points to be sampled both times (63.2^2).
So 40% is the absolute minimum overlap you’d expect to see, if the points were far enough from one another that they each had a unique bounding box. As the kernel bandwidth increased, you would increasingly start to see neighboring sets of points showing up inside one another’s bounding boxes, and this number would rise steadily toward 100%.
If we’re seeing 40% overlap, then that indicates to me that most of the bounding boxes have a single point inside them. At that point, the bounding boxes aren’t actually doing anything. Samples from inside the boxes are so close to the observed data points that they might as well be replicas of them.
I get similar results if instead of resampling the points, I add an invisibly tiny amount of noise to them (e.g. Gaussian noise with sd of 1% of the observed sd, see code below).
Long story short, I’m not sure how your method is estimating the kernel bandwidth, but I’m pretty confident that the boxes are much smaller than they should be. Keep in mind that with uniform kernels, the model is assigning zero likelihood to anything outside the box. Assigning zero likelihood to things that happen means that the model has infinite deviance. In general, smoothing out model predictions to avoid scenarios with infinite deviance tends to be a good strategy.
————-
With regard to using a classifier, you say:
>what you are proposing will work very poorly on high-dimensional data because nearly all random points will be classified ‘out’
I think that’s only true if your classifier tries to hug the points unreasonably closely.
If your species of interest occurs in half the space along each dimension (which seems fairly reasonable, given that we’re only including points where the species was observed in the first place) then we’ll be able to retain one out of every 1024 samples in a 10-dimensional space. My laptop could probably generate and classify a million samples per minute once the SVM was trained, so that gives us a few thousand usable samples before I’ve had long enough to get bored. If the species only lived in the quarter of the space along each dimension, then running something like this overnight wouldn’t be the end of the world, either.
Things would still scale exponentially, which isn’t sustainable, but ten dimensions should be enough for anyone, right? Plus, this is all assuming that no one is able to do anything cleverer like sampling from inside a convex hull or sampling in a transformed space or using MCMC.
——–
#################################
library(dismo)
library(hypervolume)
data(Anguilla_train)
set.seed(1) # Set seed for reproducibility
# Pull out environmental variables where eel was present and scale.
# Drop non-environmental variables, factors, & columns with missing values
x = scale(
Anguilla_train[Anguilla_train$Angaus == 1, -c(1, 2, 13, 14)]
)
# x is scaled, so this is
x_jittered = x + rnorm(length(x), sd = .01)
v1 = hypervolume(
x,
bandwidth = estimate_bandwidth(x),
reps=20000,
quantile=0
)
v2 = hypervolume(
x_jittered,
bandwidth = estimate_bandwidth(x_jittered),
reps=20000,
quantile=0
)
set = hypervolume_set(v1, v2, reduction_factor=.05, check_memory=FALSE)
# Check overlap between hypervolumes: should be close to one.
set@HVList$Intersection@Volume / v2@Volume
set@HVList$Intersection@Volume / v1@Volume
Hi Dave,
Thanks again for engaging with this. I see you’ve also sent a separate email, so let’s take the rest of the discussion offline.
First, about the kernel bandwidth – the estimator we use isn’t guaranteed to be optimal, as we note in the documentation. Most of our own analyses have been done using fixed bandwidth values.
Second, about the low estimates – I am not sure if 40% overlap really is the null expectation. The guts of the overlap algorithm is a n-ball test, where random points in one hypervolume are checked to see if they are ‘close enough’ to at least one point in the other hypervolume, and vice-versa. This method of course has an error rate associated with it, where sometimes points will be inferred ‘out’ when they should be ‘in’ because the randomly uniform points are by chance further apart than expected. I’m guessing this also is downbiasing some of the estimates. Doing systematic studies would be very interesting.
Third, about the SVM approach – you’ve written to me about this, and I look forward to more discussions over email.
Amazing package! Love it! Thank you!
I’m having a play around with it now, and I noticed that just printing objects in the “Hypervolume” class (output from the hypervolume function) will by default print everything in it. I would recommend maybe writing a custom print/show method, otherwise users might crash their R session if they print objects with a lot of data in them. It might also be nice to have the call stored as a slot in the object so users can see how a given hypervolume object was made.
Here’s a quick and dirty attempt at such a show method, feel free to use/change/disregard:
function(x, digits=max(3L, getOption(“digits”) – 3L), …) {
# print object class
cat(“Object of class ‘Hypervolume’\n”)
# print call – call not present code but maybe in later versions?
# cat(“\nCall:\n”, paste(deparse(x$call), sep = “\n”, collapse = “\n”), “\n\n”, sep = “”)
# print values
print.default(format(matrix(c(x@Name, x@Dimensionality, x@Volume, x@PointDensity, x@RepsPerPoint), ncol=1,
dimnames=list(c(“Name:”,”Dimensionality:”,”Volume:”, “PointDensity:”, “RepsPerPoint:”), “”)), digits = digits), quote=FALSE)
cat(“Bandwidth:\n”)
print.default(format(matrix(x@Bandwidth,nrow=1, dimnames=list(c(“”), NULL)), digits = digits), quote = FALSE)
cat(“Quantile Threshold:\n”)
print.default(format(c(Desired=x@QuantileThresholdDesired, Obtained=x@QuantileThresholdObtained), digits = digits), print.gap = 2L, quote = FALSE)
}
Thanks again!
Thanks for sharing this suggestion! I will probably release an updated version of the package in the next week as more comments like this come in, and we work through some of the other issues recently raised.
I agree with former comments, that is a truely amazing R package. Thanks for sharing it.
I have also tried some of your functions with my own data and quickly realized that the ratio between number of dimensions and number of occurrences is definitely affecting the measured overlap as you pointed out in your discussion with Dave. Very interesting discussion by the way, though I’m not sure that understood it all 😉
About the bandwidth thing, you mentionned both in your discussion with Dave and in the help file of the hypervolume R package that using the function estimate_bandwidth() is possible but not recommended. Hence, you recommend using a fixed bandwidth value for all dimensions. However, I’m not sure to understand properly how to choose an ok fixed bandwidth value. I understand that it relates to the size of the box kernel but then I have no idea how to set this distance. Do you have any recommendations? By the way, shall the value be expressed in the same unit as the dimensions (cf. the scaled variables) or as a proportion of the range covered by the occurrence data along each dimension? I don’t know if I express myself properly, I apologize if this is unclear.
PS: Awesome blog and very nice pics.
Hi Jonathan, thanks for your comments! Hopefully we’ll have more insight on dimensionality soon. We currently have Miguel Mahecha working on some sensitivity analyses for our metric and others.
Setting the bandwidth with a fixed value is tricky, and we don’t have any hard and fast rules (which is why you didn’t see any in the paper). You have to choose a value that balances between on the one hand, padding data to reflect unmeasured but real possible values and on the other hand, constraining data to not include unrealistic parameter combinations. At some level you can estimate this from the data but at a deeper level it has to be a quantity determined by a human – how certain are you, really? We’ve taken two approaches so far: first, choosing a value that provides good ‘filling’ of holes we think are simply unmeasured points, then assessing the sensitivity of results to variation around this value; and second, choosing a value that produces good correlation between hypervolume and convex hull volume. This latter approach is only reasonable if of course you believe the dataset doesn’t have holes or outliers in it. I hope this helps get you started thinking about the issue.
Lastly, regarding the units of the bandwidth – the units are the same as the actual data. So if your data axes are all in standard deviations, then the bandwidth is also in standard deviations. And remember that each axis is given a different bandwidth value, so if your axes do have different units (strongly not recommended!) your bandwidth vector components will too.
Hi Benjamin, thanks for your reply and explanations.
Reblogged this on Jonathan Lenoir and commented:
A very intersting approach from Benjamin Blonder to explore species ecological niche
So, this might be a naive question, but it seems to me the problem breaks up in two parts
1) quantifying the environmental niche (hypervolume) of species
2) calculating their niche overlap
It seems reasonable or at least the most simple solution to apply Monte-Carlo integration for 2), but for 1), why wouldn’t I use standard SDM (with cutoff) or, if the ratio of data/niche dimension is unfavorable, a classifier that can deal with that like SVMs or alike for that? Those algorithms are well understood and supported in R.
Hi Florian,
Thank you for your question. We think our approach provides value in several contexts: it unifies different niche-related problems (sampling and geometry) and provides an intuitive way to operationalize the Hutchinsonian niche concept. If you are only interested in sampling applications (e.g. species distribution modeling with a threshold) then our approach can match other algorithms such as GBM and GLM. However it provides nothing fundamentally new or different relative to these other approaches. The real advantage comes in when one wishes to also ask questions about niche volume or geometry, e.g. shape and overlap. I don’t think there are yet many good ways to resolve this latter problem, except for perhaps convex hulls – and we discuss the downside of that method in the paper.
I hope this helps clarify our intent – please write again if you want to discuss further. I don’t see our approach replacing SDM algorithms for their current applications, but rather opening up a new set of questions.
Hi, sorry, I’m still struggling with that – what do you mean but unifying “sampling and geometry”? If I do a logistic regression, I do get a description of something like the realized niche, right, in the sense that I get the environmental (or whatever) parameters under which I would expect the species to be present. If I want, I can include any sampling model as a hierarchical model. And once I have the niche mapped for any species, I sure can calculate the niche overlap, I mean, I just need to look at the overlapping areas of the fitted regression in environmental space?
Hi Florian,
Let me try to explain more. I hope I am understanding your question properly.
First, It’s true that you could do something like a logistic regression to model a niche. But as we discuss in the paper, that kind of model may not have the properties that we think are important for a hypervolume, e.g. does not have an infinite range of axis values for which the species can occur. Such a model would make it difficult to define the boundaries of a hypervolume. Additionally, calculating exactly the volume of hyperspace occupied by any given niche might not be trivial for some of these ENM/SDM algorithms – we provide one way to do it using our thresholded KDE approach.
Second, I think that the overlap calculation is more difficult than you would imagine in high dimensions. We are essentially doing what you propose, looking at overlapping areas of two different models, but using an algorithm that scales reasonably well to large datasets. For example even convex polytope intersection calculations is hard, and there is no reason to expect that hypervolumes should be convex. The closest ecological work I’m aware of relating to high-dimensional overlap is
Villéger, S., Novack-Gottshall, P. M., & Mouillot, D. (2011). The multidimensionality of the niche reveals functional diversity changes in benthic marine biotas across geological time. Ecology Letters, 14(6), 561–568. doi:10.1111/j.1461-0248.2011.01618.x
I hope this helps to clarify further!
Ben
[…] Some blog discussion here […]
Reblogged this on Deterritorial Investigations Unit and commented:
via http://ecologywithoutnature.blogspot.com/2016/08/niches-as-hypervolumes.html